Public Member Functions | Static Public Member Functions | List of all members
Opm::FlashModel< TypeTag > Class Template Reference
Flow Models » Flash

A compositional multi-phase model based on flash-calculations. More...

#include <flashmodel.hh>

Inheritance diagram for Opm::FlashModel< TypeTag >:
Inheritance graph

Public Member Functions

 FlashModel (Simulator &simulator)
 
std::string primaryVarName (unsigned pvIdx) const
 Given an primary variable index, return a human readable name. More...
 
std::string eqName (unsigned eqIdx) const
 Given an equation index, return a human readable name. More...
 
Scalar primaryVarWeight (unsigned globalDofIdx, unsigned pvIdx) const
 Returns the relative weight of a primary variable for calculating relative errors. More...
 
Scalar eqWeight (unsigned globalDofIdx, unsigned eqIdx) const
 Returns the relative weight of an equation. More...
 
void registerOutputModules_ ()
 
 FlashModel (Simulator &simulator)
 
std::string primaryVarName (unsigned pvIdx) const
 Given an primary variable index, return a human readable name. More...
 
std::string eqName (unsigned eqIdx) const
 Given an equation index, return a human readable name. More...
 
void registerOutputModules_ ()
 
bool phaseIsConsidered (unsigned) const
 Returns true iff a fluid phase is used by the model. More...
 
void globalPhaseStorage (EqVector &storage, unsigned phaseIdx)
 Compute the total storage inside one phase of all conservation quantities. More...
 

Static Public Member Functions

static void registerParameters ()
 Register all run-time parameters for the immiscible model. More...
 
static std::string name ()
 
static void registerParameters ()
 Register all run-time parameters for the immiscible model. More...
 

Detailed Description

template<class TypeTag>
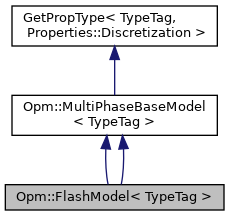
class Opm::FlashModel< TypeTag >

A compositional multi-phase model based on flash-calculations.

This model assumes a flow of $M \geq 1$ fluid phases $\alpha$, each of which is assumed to be a mixture $N \geq M$ chemical species (denoted by the upper index $\kappa$).

By default, the standard multi-phase Darcy approach is used to determine the velocity, i.e.

\[ \mathbf{v}_\alpha = - \frac{k_{r\alpha}}{\mu_\alpha} \mathbf{K} \left(\mathbf{grad}\, p_\alpha - \varrho_{\alpha} \mathbf{g} \right) \;, \]

although the actual approach which is used can be specified via the FluxModule property. For example, the velocity model can by changed to the Forchheimer approach by

template<class TypeTag>
struct FluxModule<TypeTag, TTag::MyProblemTypeTag> { using type = Opm::ForchheimerFluxModule<TypeTag>; };
Opm::ForchheimerFluxModule
Specifies a flux module which uses the Forchheimer relation.
Definition: forchheimerfluxmodule.hh:62

The core of the model is the conservation mass of each component by means of the equation

\[ \sum_\alpha \frac{\partial\;\phi c_\alpha^\kappa S_\alpha }{\partial t} - \sum_\alpha \mathrm{div} \left\{ c_\alpha^\kappa \mathbf{v}_\alpha \right\} - q^\kappa = 0 \;. \]

To determine the quanties that occur in the equations above, this model uses flash calculations. A flash solver starts with the total mass or molar mass per volume for each component and, calculates the compositions, saturations and pressures of all phases at a given temperature. For this the flash solver has to use some model assumptions internally. (Often these are the same primary variable switching or NCP assumptions as used by the other fully implicit compositional multi-phase models provided by eWoms.)

Using flash calculations for the flow model has some disadvantages:

  • The accuracy of the flash solver needs to be sufficient to calculate the parital derivatives using numerical differentiation which are required for the Newton scheme.
  • Flash calculations tend to be quite computationally expensive and are often numerically unstable.

It is thus adviced to increase the target tolerance of the Newton scheme or a to use type for scalar values which exhibits higher precision than the standard double (e.g. quad) if this model ought to be used.

The model uses the following primary variables:

  • The total molar concentration of each component: $c^\kappa = \sum_\alpha S_\alpha x_\alpha^\kappa \rho_{mol, \alpha}$
  • The absolute temperature $T$ in Kelvins if the energy equation enabled.

This model assumes a flow of $M \geq 1$ fluid phases $\alpha$, each of which is assumed to be a mixture $N \geq M$ chemical species (denoted by the upper index $\kappa$).

By default, the standard multi-phase Darcy approach is used to determine the velocity, i.e.

\[ \mathbf{v}_\alpha = - \frac{k_{r\alpha}}{\mu_\alpha} \mathbf{K} \left(\mathbf{grad}\, p_\alpha - \varrho_{\alpha} \mathbf{g} \right) \;, \]

although the actual approach which is used can be specified via the FluxModule property. For example, the velocity model can by changed to the Forchheimer approach by

template<class TypeTag>
struct FluxModule<TypeTag, TTag::MyProblemTypeTag> { using type = Opm::ForchheimerFluxModule<TypeTag>; };

The core of the model is the conservation mass of each component by means of the equation

\[ \sum_\alpha \frac{\partial\;\phi c_\alpha^\kappa S_\alpha }{\partial t} - \sum_\alpha \mathrm{div} \left\{ c_\alpha^\kappa \mathbf{v}_\alpha \right\} - q^\kappa = 0 \;. \]

To determine the quanties that occur in the equations above, this model uses flash calculations. A flash solver starts with the total mass or molar mass per volume for each component and, calculates the compositions, saturation and pressures of all phases at a given temperature. For this the flash solver has to use some model assumptions internally. Here a constant pressure, constant temperature, two-phase flash calculation method is used.

Constructor & Destructor Documentation

◆ FlashModel() [1/2]

template<class TypeTag >
Opm::FlashModel< TypeTag >::FlashModel ( Simulator &  simulator)
inline

◆ FlashModel() [2/2]

template<class TypeTag >
Opm::FlashModel< TypeTag >::FlashModel ( Simulator &  simulator)
inlineexplicit

Member Function Documentation

◆ eqName() [1/2]

template<class TypeTag >
std::string Opm::FlashModel< TypeTag >::eqName ( unsigned  eqIdx) const
inline

Given an equation index, return a human readable name.

Parameters
eqIdxThe index of the conservation equation of interest.

◆ eqName() [2/2]

template<class TypeTag >
std::string Opm::FlashModel< TypeTag >::eqName ( unsigned  eqIdx) const
inline

Given an equation index, return a human readable name.

Parameters
eqIdxThe index of the conservation equation of interest.

◆ eqWeight()

template<class TypeTag >
Scalar Opm::FlashModel< TypeTag >::eqWeight ( unsigned  globalDofIdx,
unsigned  eqIdx 
) const
inline

Returns the relative weight of an equation.

Parameters
globalVertexIdxThe global index of the vertex
eqIdxThe index of the equation

◆ globalPhaseStorage()

template<class TypeTag >
void Opm::MultiPhaseBaseModel< TypeTag >::globalPhaseStorage ( EqVector &  storage,
unsigned  phaseIdx 
)
inlineinherited

Compute the total storage inside one phase of all conservation quantities.

Parameters
storageStores the total amount of each conserved quantity inside the domain.
phaseIdxThe index of the fluid phase of interest.

References Opm::ThreadedEntityIterator< GridView, codim >::beginParallel(), Opm::ThreadedEntityIterator< GridView, codim >::increment(), Opm::ThreadedEntityIterator< GridView, codim >::isFinished(), and Opm::ThreadManager< TypeTag >::threadId().

◆ name()

template<class TypeTag >
static std::string Opm::FlashModel< TypeTag >::name ( )
inlinestatic

◆ phaseIsConsidered()

template<class TypeTag >
bool Opm::MultiPhaseBaseModel< TypeTag >::phaseIsConsidered ( unsigned  ) const
inlineinherited

Returns true iff a fluid phase is used by the model.

Parameters
phaseIdxThe index of the fluid phase in question

◆ primaryVarName() [1/2]

template<class TypeTag >
std::string Opm::FlashModel< TypeTag >::primaryVarName ( unsigned  pvIdx) const
inline

Given an primary variable index, return a human readable name.

Parameters
pvIdxThe index of the primary variable of interest.

◆ primaryVarName() [2/2]

template<class TypeTag >
std::string Opm::FlashModel< TypeTag >::primaryVarName ( unsigned  pvIdx) const
inline

Given an primary variable index, return a human readable name.

Parameters
pvIdxThe index of the primary variable of interest.

◆ primaryVarWeight()

template<class TypeTag >
Scalar Opm::FlashModel< TypeTag >::primaryVarWeight ( unsigned  globalDofIdx,
unsigned  pvIdx 
) const
inline

Returns the relative weight of a primary variable for calculating relative errors.

Parameters
globalDofIdxThe global index of the degree of freedom
pvIdxThe index of the primary variable

◆ registerOutputModules_() [1/2]

template<class TypeTag >
void Opm::FlashModel< TypeTag >::registerOutputModules_ ( )
inline

References Opm::MultiPhaseBaseModel< TypeTag >::registerOutputModules_().

◆ registerOutputModules_() [2/2]

template<class TypeTag >
void Opm::FlashModel< TypeTag >::registerOutputModules_ ( )
inline

References Opm::MultiPhaseBaseModel< TypeTag >::registerOutputModules_().

◆ registerParameters() [1/2]

template<class TypeTag >
static void Opm::FlashModel< TypeTag >::registerParameters ( )
inlinestatic

Register all run-time parameters for the immiscible model.

References Opm::MultiPhaseBaseModel< TypeTag >::registerParameters(), Opm::VtkCompositionModule< TypeTag >::registerParameters(), Opm::VtkDiffusionModule< TypeTag >::registerParameters(), and Opm::VtkEnergyModule< TypeTag >::registerParameters().

◆ registerParameters() [2/2]

template<class TypeTag >
static void Opm::FlashModel< TypeTag >::registerParameters ( )
inlinestatic

Register all run-time parameters for the immiscible model.

References Opm::MultiPhaseBaseModel< TypeTag >::registerParameters(), Opm::VtkCompositionModule< TypeTag >::registerParameters(), Opm::VtkDiffusionModule< TypeTag >::registerParameters(), Opm::VtkEnergyModule< TypeTag >::registerParameters(), and Opm::VtkPTFlashModule< TypeTag >::registerParameters().

The documentation for this class was generated from the following files: